In no way can I replicate the richness and depth of the conversations (I am immensely thankful for all of the participation of attendees!) and atmosphere from the two practicums where I spoke, but I pray that—whether you attended the Eugene or Albany (Oregon) practicums, attended a CC practicum in another city, or were unable to attend—these abbreviated notes are helpful or inspiring. (I am sharing my personal speaking notes, so they will not necessarily correspond with other practicums.)
I posted about the purpose of the practicums at this link, the idea of Copiousness at the end of this link, and the main themes of classical education and teaching mathematics within that framework in Part 1 of this series, so we’ll jump straight to Cosmos in this post. (If you are interested in the basics of Classical Conversations, check out this link in which I share details of our own experience.) (I’d share my opening joke, but no one laughed. Ha!)
Day 1
Theme: Cosmos (Words matter.)
In all my reading (in the spirit of copiousness) leading up to the practicum, I continually came across the word cosmos. I had a general idea of what cosmos meant, but as I personally have been on a “words matter” focus lately, I decided to look up the definition.
A cosmos is an orderly or harmonious system. The word derives from the Greek term κόσμος (kosmos), meaning literally "order" or "ornament" and metaphorically "world,” and is diametrically opposed to the concept of chaos.
While we’re at it, let’s look up the definition of ornament: (Merriam-Webster)
2a. something that lends grace or beauty
3: one whose virtues or graces add luster to a place or society
Order. (Form. Structure. Truth.) Ornament. (Beauty. Harmony. Grace. Virtue.)
Order + Beauty (literally) = World (metaphorically)
(We’re really starting at the very beginning, here.)
Genesis 1:1-2 In the beginning God created the heavens and the earth. Now the earth was formless and empty, darkness was over the surface of the deep, and the Spirit of God was hovering over the waters.
Formless. And what did God do? Created form: separated light and darkness, waters and sky, land and seas.
Empty. And once the form established, he filled the place with beauty: plants, stars, birds, sea creatures, animals, man.
Genesis 2:1 Thus the heavens and the earth were completed in all their vast array.
(Words matter!)
Array: verb (used with object):
1. to place in proper or desired order
2. to clothe with garments, especially of an ornamental kind; dress up; deck out.
And, as Leigh Bortins says, that’s how you teach everything to everybody. Figure out what the form is, and then you have all the content in the world to make it creative, beautiful!
Sentence forms
Latin ending forms
Math formulas
The structure of story
You can put in whatever content you wish once you know the form. The content is what makes it unique and interesting.
This includes the form of classical education.
Day 1: Focus on Grammar
Grammar is the first art or tool of the trivium. This is the stage of input. Grammar is not just the study of the structure of language, it is defined as the “science of vocabulary” (Leigh Bortins, The Core: Teaching Your Child the Foundations of Classical Education, page 48). The student (of any age) must first internalize (by exposure and mastery) the vocabulary, definitions, facts, stories, ideas, names, dates, and rules of a subject or skill.
“No matter what your children’s strengths and weaknesses are, or their likes and dislikes, or their gifts and talents—their brains want to gather, sort, and store, and retrieve information.” (The Core, page 52)
“It is not surprising that, for the Greek mind, the Muses—of epic, history, astronomy, music, dance, tragedy, comedy, lyric poetry, and sacred poetry—should be daughters of Memory.” (Anthony Esolen, Ten Ways to Destroy the Imagination of Your Child, page 9)
“One simple and immutable fact about the human brain is that you can’t get something out of it that isn’t there to start with. Supernatural inspiration notwithstanding, human beings in general—and children in particular—really can’t produce... thoughts or concepts that they haven’t first experienced and stored. In other words, we cannot think a thought we don’t have to begin with. Even the most unique, creative, and extraordinary ideas can only exist as a combination and permutation of previously learned bits of information.” (Andrew Pudewa, 1 Myth, 2 Truths)
“There are times when memorization is out of favor in education. Some might say that “rote memorization” is not appropriate as a teaching strategy. “Rote memorization,” however, is loaded language, biased against the discipline and effort required to learn things permanently. There is nothing wrong with challenge. We must remember that the alternative to remembering is forgetting, and when we teach something as important as grammar, that will be needed for one’s entire life, the ban on memorization makes little sense. There are areas of knowledge that should be memorized, and in the past, there was a better term for it: to learn by heart.” (Michael Clay Thompson)
“But more than that, we would desire to bring children into the garden of created being, and thought, and expression. Caldecott reminds us that for the medieval schoolmen, as for Plato, education was essentially musical, an education in the cosmos or lovely order that surrounds us and bears us up. Thus when we teach our youngest children by means of rhymes and songs, we do so not merely because rhymes and songs are actually effective mnemonic devices. We do so because we wish to form their souls by memory: we wish to bring them up as rememberers, as persons, born, as Caldecott points out, in certain localities, among certain people, who bear a certain history, and who claim our love and loyalty.” (Anthony Esolen, author of Ten Ways to Destroy the Imagination of Your Child, in the Foreword from Beauty in the Word: Rethinking the Foundations of Education by Stratford Caldecott)
Mathematics
“The sheer amount of information available in every discipline is far too great to be mastered by one person even in a lifetime. The purpose of an education is not merely to communicate information, let alone current scientific opinion, nor to train future workers and managers. It is to teach the ability to think, discriminate, speak, and write, and, along with this, the ability to perceive the inner, connecting principles, the intrinsic relations, the logoi, of creation, which the ancient Christian Pythagorean tradition...understood in terms of number and cosmic harmony.” (Stratford Caldecott, Beauty for Truth's Sake: On the Re-enchantment of Education, page 28)
Michael S. Schneider writes, “Numbers are a map of the beautiful order of the universe, the plan by which the divine Architect transformed undifferentiated Chaos into orderly Cosmos.” (Beauty for Truth’s Sake, page 54)
God spoke in words (His very name “I AM” is a subject and a predicate, the form of language, Exodus 3:14), but he also spoke in math.
“Mathematics is the language of science, but it is also the hidden structure behind art…, and its basis is the invisible Logos of God.” (Beauty for Truth’s Sake, page 30)
Galileo Galilei (1564–1642) said, "The universe cannot be read until we have learned the language and become familiar with the characters in which it is written. It is written in mathematical language, and the letters are triangles, circles and other geometrical figures, without which means it is humanly impossible to comprehend a single word. Without these, one is wandering about in a dark labyrinth."
“The laws of nature are but the mathematical thoughts of God.” ~Euclid
(Words matter!) The word mathematics comes from the Greek μάθημα (máthēma), which, in the ancient Greek language, means "that which is learnt", "what one gets to know," hence also "study" and "science", and in modern Greek just "lesson."
From Merriam-Webster, the definition of MATHEMATICS: the science of numbers and their operations, interrelations, combinations, generalizations, and abstractions and of space configurations and their structure, measurement, transformations, and generalizations. (Whew!!)
Another source defined math as the study of relationships using numbers.
Mathematics is the abstract study of quantity, structure, space, change, and many other topics. It has no generally accepted definition.
Let’s talk about a brief history of math.
Why?
“An integrated curriculum must teach subjects, and it must teach the right subjects, even mathematics and the hard sciences, within the history of ideas, which is the history of our culture. Every subject has a history, a drama, and by imaginatively engaging with these stories we become part of the tradition.” (Beauty for Truth’s Sake, page 28)
From Mathematics: The Science of Patterns by Keith Devlin:
Up until c. 500 B.C. mathematics was indeed the study of number. During the period of Egyptian and Babylonian mathematics, it consisted almost solely of utilitarian arithmetic or counting.
500 B.C. to 300 A.D., the era of Greek mathematics was primarily concerned with measurement and geometry—number and shape. Not just utilitarian, mathematics was regarded as an intellectual pursuit having both aesthetic (beauty!) and religious elements. From the Greeks we have Euclid’s Elements.
In the middle of the seventeenth century, Newton and Leibniz independently invented calculus—essentially the study of motion and change—making it possible to study physics and the motion of planets, among other things. So mathematics became the study of number, shape, motion, change, and space.
In the year 1900, all the world’s mathematical knowledge would have fit into about 80 books. Today it would take maybe 100,000 volumes to contain all known mathematics.
As you can imagine, many quite new branches of mathematics have sprung up.
[Mark Twain said “We could use up two Eternities in learning all that is to be learned about our own world and the thousands of nations that have arisen and flourished and vanished from it. Mathematics alone would occupy me eight million years.”]
Many mathematicians agree that mathematics can be considered the science of patterns. Mathematicians examine abstract patterns using symbolic notation—mathematical language.
The History of Counting is a fantastic picture book introduction to the history of counting across cultures.
The quadrivium consists of arithmetic (pure number), geometry (number in space), music (number in time), and astronomy (number in space and time) (Beauty for Truth’s Sake, page 24)). Our focus is arithmetic.
There are only are 3 (three!) basic things to learn in arithmetic…everything else is just more complex combinations of these three categories:
Numbers (8), operations (6), and laws (4). That’s it!
This is our FORM!
Math in a nutshell: “There are digits, you do things with them, and they follow laws.” Leigh Bortins
So let’s begin with the definitions. You cannot have a conversation about something if you don’t have words to use—not “thingy”! Kids soak up vocabulary. If they can say Tyrannosaurus Rex, they can say denominator. It’s adults who are intimidated!
(Understanding Mathematics: From Counting to Calculus is a great all-in-one resource for adults who are in the process of redeeming their education or as a teaching reference.)
A Number is the IDEA that I have three of something.
A Numeral is the SYMBOL used to express the idea. (For example, we use the heart symbol to express the idea of love.)
We are talking about real numbers today. Real numbers can be written as a fraction (as opposed to irrational #s which do not have a ratio—cannot be written as a fraction—such as pi).
Natural Numbers are the counting numbers. They are positive and exclude 0. 1, 2, 3, 4, 5… and so on.
Whole Numbers are the counting numbers and 0. 0, 1, 2, 3, 4… This is easy to remember if you look at the word Wh0le and think of the o as a 0.
Integers are the whole numbers and their opposites (including 0). …-4, –3, –2, –1, 0, 1, 2, 3, 4…
A number located in between integers on the number line is called a Decimal. Add a decimal point and add numbers to the right to indicate a decimal. This is part of our base 10 system. A natural number can be expressed as a decimal by adding .0
Fractions. A fraction is a number in the form of a over b. the line represents division. A fraction is simply an integer or decimal number, prior to completing the division. The top number is called the numerator. The bottom number is called the denominator. Also called a ratio. (A fraction may also be defined as a ratio of numbers, where a ratio is just the division relationship a/b.)
A proper fraction has a value less than one (the numerator is less than the denominator).
An improper fraction has a value greater than one (the numerator is greater than the denominator) such as 6/1 or six divided by 1 equals 6.
Mixed numbers include an integer and a ratio. Could 6 be expressed as a mixed number in different ways? Yes. The integer of a mixed number will be a 0 if the value is less than one.
Percent. % symbols mean the number was multiplied by 100, so divide by 100 to return to a non-percent number.
Scientific Notation is used when working with very large or very small numbers and is a very specific form. In scientific notation a number is rewritten as a value between 1 and (less than) 10 (a digit in the one’s place) expressed as a decimal, multiplied by a factor of 10.
10 to a positive power means that you move the decimal that many places to the right (used for large numbers). 10 to a negative power means that you move the decimal that many places to the left (used for small numbers).
Anything to the 0 power = 1, so the number three expressed in scientific notation would be 3.0 x 10 to the 0 power or 10^0.
Why? Here is one example of why it works:
I challenge you to express a number in as many different ways as possible. This is a fun activity to do with kids. The boys and I filled a page with symbols expressing the value of the number six, including Roman numerals, percent, tally marks, stick figure people, fraction “pies,” dots on a die, and various numerical expressions (numbers and operations).
“When I was a boy, we had to memorize the multiplication tables in the second grade, up to 12 x 12 = 144. Let’s set aside the fact that it takes a deal of intelligence and some ingenuity to accomplish that task. Forget that you would have to learn that anything multiplied by 5 ends in 5 or 0, alternately. Forget that if you were sharp you’d see that odd times odd is odd, and everything else is even. Forget the patterns showing up among the 2s, 4s, and 8s. Forget the nice progression in the 9s, with the tens digit gaining one and the ones digit dropping it: 09, 18, 27, and so forth. What that memorization did was to free you up to become comfortable with numbers themselves, and with the structure of arithmetic. Once you had done that, you could play with numbers creatively, long before you’d ever suspected the existence of algebra or calculus, with their toboggan curves and their infinite series and their radio waves, their transcendental numbers and the mysterious i, the square root of –1, whose existence we must leave to philosophers to determine.” (Anthony Esolen, Ten Ways to Destroy the Imagination of Your Child, page 20)
And another interesting dive into the meaning of words:
“In English, integrity is a word related to a number of other familiar ones. It is built from the root word, integer. Now, as most of us learned in early math, an integer is a whole number, as in 1,2,3,3- that is, whole numbers as opposed to fractions. They are whole or complete numbers, not parts of a whole.”
Integer
2. A complete entity.
[1500–10; < Latin: untouched, hence, undivided, whole]
In·teg·ri·ty
1. Steadfast adherence to a strict moral or ethical code.
2. The state of being unimpaired; soundness.
3. The quality or condition of being whole or undivided; completeness.
[Middle English integrite, from Old French, from Latin integrits, soundness, from integer, whole, complete]
“In relating the word integrity to our lives, it describes an uncompromised character, an unjaded soul, an unsullied heart, an undivided mind. It requires the maintenance of our hearts in entirety before the Lord. David said: "Unite my heart to fear Your name." Those words say, "God, draw the strands of my heart so firmly tight and in such reverence before Your throne, that I will be kept wholly and entirely aligned with You."

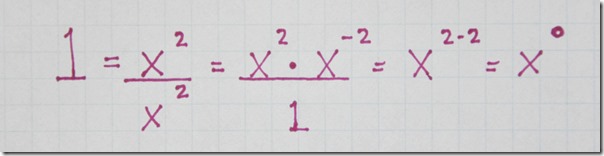
1 comment:
Heidi, I am soooooooooo glad to review all that complicated information I received at your "praticum" in Albany. Some of it I had never heard, now some I had heard now makes sense. Thanks so much for printing it all out here so maybe I can get it all more firmly in my head. Grandma
Post a Comment