Notes, Quotes, Links, and More ~ Part 4

Part 1 (Basic Overview: Classical Education and Mathematics)

Part 2 (Day 1 Notes: Cosmos!)

Part 3 (Fibonacci)

 

Day 2: Playing with Cosmos (Poetry)

Octoproblem by Kenn Nesbitt (poem at link)

What is the grammar one must know to get the joke? (Grammar students: math facts “pi,” Latin vocab “Octo,” Latin declensions (plural second declension)).

[Because words matter, I discovered that the plural form of octopus is actually octopuses (or occasionally octopodes). Octopus is not a simple Latin word of the second declension, but a Latinized form of the Greek word oktopous, and its 'correct' plural would logically be octopodes. Interesting, no?]

Reviewing Cosmos:

A cosmos is an orderly or harmonious system. The word derives from the Greek term κόσμος (kosmos), literally meaning "order" or "ornament" and metaphorically "world", and is diametrically opposed to the concept of chaos.

Order and Ornament
Truth and Grace
Mathematics and Language

Know form. Add beauty.

Array: put in order and then deck out!

“Structure—a ‘grammar’ that orders every part in its appropriate place—is important not only for the physical sciences, but for every kind of intellectual endeavor. It allows us to do more than weave a fancy from the bits and pieces of our private experience. We can, by the power of structure, weave a whole artistic universe.” Anthony Esolen, Ten Ways to Destroy the Imagination of Your Child

Let’s play with Cosmos!

We are going to try combining language and math today. (I was trying to figure out a way to tie in sentence diagramming (ha!!), but I couldn’t make it work. [After I mentioned this, a parent at the practicum shared a link to her son’s blog wherein he creates a sentence diagram of mathematical notation. It’s fantastic. I’m inspired to try one of my own—on a much, much lower level…] I really wanted to do personality types, but poetry spoke to me.

“After all, science, like poetry, begins with a search for unifying principles, and the unifying factor in creation is its relation to God.” (Stratford Caldecott, Beauty for Truth's Sake, page 29)

“What I want to suggest is that the opposition between the “cultures” of science and the arts can be overcome by teaching science and mathematics themselves at least partly according to the poetic mode. In other words, the best way to teach them is by first awakening the poetic imagination. We need to reestablish—for the sake of science as much as for the arts—a truly humane education that, in Taylor’s words, “begins with the senses, and the discovery and cultivation of harmony and beauty in the soul by way of the sense’s natural affinity for the harmonious, proportionate, and the beautiful in nature and the arts.” If children were from an early age exposed to a “musical” training in the Greek sense, if their poetic sensibility was kindled by training in the observation of nature and the learning of poetry, and if mathematics and science were taught historically, with due attention to the symbolic and beautiful properties of numbers and shapes, then we might even begin to see the birth of that “regenerate science” that Lewis prophesied.” (Beauty for Truth’s Sake, page 45)

“Additionally, because of the nature of poetry, poets are often compelled to stretch our vocabulary, utilizing words and expressions in uniquely sophisticated—but almost always correct—language patterns.” (Andrew Pudewa, 1 Myth, 2 Truths)

“When a carpenter creates, there is a sense in which he destroys the original in order to create something new. When he makes a table, he has to first destroy the tree. The author, on the other hand, does not destroy Hamlet in order to create Falstaff. This is the closest we experience creation out of nothing. Sayers is echoing the teachings of the church fathers who taught that in creating something orderly and beautiful that did not previously exist, the artist is paralleling what God did in the act of creation.” (Imago Dei and the Redemptive Power of Fantasy—Part 1 by Angelina Stanford @ Circe Institute)

Math communicates a lot of meaning through an economy of symbols—like poetry.

For example:

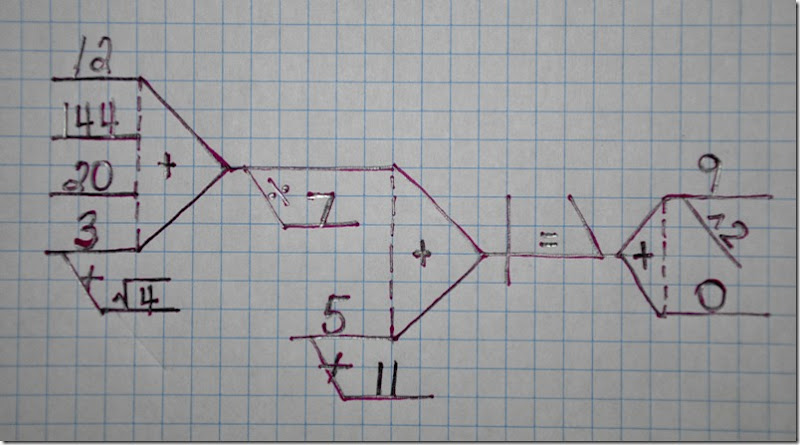
((12 + 144 + 20 + (3 * 4^(1/2))) /7) + (5 * 11) = 9^2 + 0

Some of you, through natural talent and/or practice over time have developed a set of math “eyes” and can immediately see beautiful harmony in this equation. For some of you, this is a fascinating puzzle you are itching to solve. For some of you, this equation strikes your heart with dread.

What you might not see is poetry, but it’s there. Look closely, and take a moment to let it sink in.

“A Dozen, a Gross and a Score,
plus three times the square root of four,
divided by seven,
plus five times eleven,
equals nine squared and not a bit more.”

(From Discover Magazine, attributed to John Saxon)

What grammar do you have to know to understand this poem (get the joke)? Numeracy, notation (^caret * /), operations & order of operations (which we are covering shortly), “dozen, gross, and score,” that any number to the half power = the square root of the number (I didn’t know that), the poetry FORM. Does anyone know what this specific poetry form is called?

Defining/history: A limerick is a short, humorous, often vulgar or nonsense poem. The form can be found in England as of the early years of the 18th century. It was popularized by Edward Lear in the 19th century, although he did not use the term. Even Shakespeare did in fact write limericks which can be found in two of his greatest plays - Othello and King Lear.

FORM :

A Dozen/, a Gross, and/ a Score,
Plus three times/ the square root/ of four
Divided/ by seven
Plus five times/ eleven
Equals nine squared/ and not a/ bit more.

1 stanza (like a paragraph) of 5 lines (counting).
AABBA rhyme scheme (pattern).
Lines 1, 2, 5 have three feet (like measures in music) with three syllables (or beats) each. Lines 3, 4 have two feet with 3 beats each (multiplication).
Usually anapest (ta-ta-TUM), but sometimes amphibrachic (ta-TUM-ta) (rhythm).
(This poem has a silent beat at the end of lines 1, 2, and 5—like a rest in music. And “equals” is squished into one beat.)

Considered easy to compose, historically limericks have been used by the “working class.” Not necessarily a sophisticated form of beauty, but at least there is room for creativity and enjoyment. A chance to play with form.

ETA: I thought I’d give a stab at diagramming that one. What do you think? Would you diagram it differently?

I’ll give you one more:

‘Tis a favorite project of mine
A new value of pi to assign.
I would fix it at three
For it’s simpler, you see,
Than three point one four one five nine.

Let’s try something a little different. Let’s add in some Fibonacci.

The Fibonacci sequence is named after Leonardo Fibonacci. His 1202 book Liber Abaci introduced the sequence to Western European mathematics. It is a number pattern found in nature—such as in branching in trees, the arrangement of leaves on a stem, the fruit sprouts of a pineapple, the flowering of artichoke, an uncurling fern and the arrangement of a pine cone. It also has many practical applications—the Fibonacci sequence is also the foundation of how apparel is sized (called "grading") and it’s used in knitting. There is so much more to say about it, but for now I’ll just tell you that the sequence starts with the numbers 0 and 1. Then every subsequent number is the sum of the previous two numbers. (White board!) So you have 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, and so on.

Gregory K. Pincus, a screenwriter and aspiring children's book author in Los Angeles, wrote a post on his GottaBook blog inviting readers to write "Fibs," six-line poems that used a mathematical progression known as the Fibonacci sequence to dictate the number of syllables in each line.

Your mission, should you choose to accept it, is to write a Fib and share it on the Day 3 (Rhetoric) post coming up!!

Mathematics

 

(When is 4 half of 9? Draw a horizontal line through the middle of IX.)

Operations

What is the definition of a noun? A noun names a person, place, thing, activity, or idea.

Numbers are the nouns of math. Numerals name the idea of numbers.

Operations are verbs.

We are doing something with numbers. Action.

Equations are like linking verbs. They make an assertion. This thing IS this thing. It is the idea of equality. (Harmony, not discord!)

Let’s talk about the vocabulary of operations. We cannot have a conversation without words that MEAN something. Use the correct vocabulary when you are talking about math with your kids! They will pick it up effortlessly, just as they did “ball” or “apple.” If you need a refresher, Understanding Mathematics: From Counting to Calculus is a great place to start. Often (when there are gaps in our own education) we as adults have to start at the grammar stage. And it will take more than reading the definition for these words to become part of our natural vocabulary. We have to use them in conversation. Over and over and over and over again. Repetition. Duration. (Commit to teaching these concepts to a group of adults and BAM! You’ll have intensity. Ha!)

The PURPOSE of the grammar stage, laying these foundations, is so that students have the tools they need to function in the next stage. This isn’t a parlor trick. Or entertainment when the family gets together at Christmas. We are not trying to torture our children with needless repetition. (Piano students who learn their scales to the point of muscle memory have a huge advantage when learning complex pieces of music. The scales are not the end! Basketball drills are not the end. They are a means to a higher purpose—the dialectic and rhetoric process.) It will be laborious if not impossible for our kids to have conversations about math—more complex math—when they get to Challenge if they have to learn the grammar simultaneously. And parents who become tutors—as we transition to a more rhetorical model of math in the Challenge seminar—you will not be able to facilitate discussion if you do not have the vocabulary!

When kids are having trouble with a problem and ask for help, start by asking them to define their numbers and operations. What is this? What is this asking you to do?

“Every math problem provides a micro-example for practicing the skills of learning. The students demonstrate that they have mastered the math terms used (grammar) and that they understand the rules and strategy of the problem so that they can solve the problem (dialectic). Finally, they explain how they solved the problem rhetorically, demonstrating that they understand the algorithm.” (Leigh Bortins, The Core, page 134)

I’m preaching to myself, because this is NOT something that is natural for me! But if I can learn this grammar to present at the practicum, you can learn it to teach your children. And we get to exercise our brains!! And learn more about the nature of God!

Let’s travel back in time to first grade. + - = x or * (asterisk or dot for multiplication) There are 4! ways to denote division including fractions and ratios such as 6:3. (Symbols are “operators”)

Everyone okay so far?

Addend: a number that is added to another in forming a sum.
Sum: The answer to an addition problem

Minuend: a number from which another is subtracted (the number to be diminished or made smaller; musicians think “diminuendo”)
Subtrahend: a number that is subtracted from another (sub = under like submarine)
Difference: The answer in a subtraction problem

Multiplication: The repeated addition of a certain number.
Factors: Numbers being multiplied
Product: The answer to any multiplication problem.

Dividend: The number that is being divided.
Divisor: The number that is doing the dividing.
Numerator: The number above the division sign (a).
Denominator: The number below the division sign (b).
Quotient: The answer of a division operation.

How are we doing?

How about > and < or >? “Does not equal” symbol.

Subtraction is just like addition, but you move backwards on the timeline.

Division is the opposite of multiplication, right?

Exponents (two ways to write). 4^ (caret) 2 = 4x4
Exponents: Just as multiplication is repeated addition of a number, exponents are a shortcut notation when there is a need to multiply the same number together many times. It is just a specific form of multiplication.
Base: The number in an exponent notation to be multiplied.

Roots (symbol) or radicals. Square root of 16 (What number multiplied by itself equals 16?)
Opposite of exponents. Just a specific form of division.

Order of operations: PE MD AS (Please Excuse My Dear Aunt Sally) Parentheses, Exponents. Multiplication and Division (from left to right). Addition and Subtraction (from left to right).

Just as we were challenged on day 1 to express a numerical value in different ways (fraction, decimal, percent, scientific notation—even Roman numerals, tally marks, dots on dice, pictures, etc.), now we can express a single numerical value using the form of operations. As the complexity increases, so does the creativity. We have more ways to express the same value!

12/2
2+1+3
1 x 6
(3.0 x 10^0) + (3.0 x 10^0)
127 - 121
The square root of 36 or 36^(1/2)
1 6/6 + 2 12/6
800% – 200%
3^2 - 3^1

Playing Board Slam is an entertaining way to become comfortable with manipulating numbers and operations.

Write the numbers 1-36 (in rows of 6) on a white board or a piece of paper. (You can go up to 100 or higher if you have math dice with numbers up to 12.)

Roll three dice and write the numbers on the board. Players are challenged to use all three numbers once each, in any order, with any operations (or order of operations), to make up a numerical value. They state the value (and how they got it), and that number is crossed off the board. Players come up with as many numerical expressions as possible. The goal of the game is to cross off as many numbers as possible with one roll of the dice, or cross off all numbers with as few rolls of the dice as possible.

This game can be used at any level. Start with addition and subtraction and work your way up. Adults and older students find the game challenging with exponents (must use one of the given numbers as an exponent, or agree to use a “free” zero), square roots, factorials (4! = 4 x 3 x 2 x 1). Try it for family game night!

Ready to move beyond base 10?

Although the concepts are more simplistic (only halving and doubling), I find Ethiopian math takes me more time to solve.

Here’s a method for more speed: